At the end of the last post we had a pretty solid memory allocator. Where does that take us though? Well in some cases, making hundreds of small allocations can lead to thousandfold improvements. Today, we reach for performance!

Wait a minute… this has nothing to do with kernel dev

Guess again! SnowflakeOS’s window manager is in the kernel^[1]. It is quite rude for a system call to take a whole second to return, and sadly this is the situation we found ourselves in.

How did we end up like this?

It’s relatively easy to make a slow window manager, which is what we did. Just redraw all of your windows when you wish to redraw one, hell, redraw your whole desktop when you move the mouse!

Of course, don’t forget to use an off-screen buffer so that you can copy the whole screen buffer twice every chance you get.

To be fair, I don’t write window managers everyday :)

Hello clipping my old friend

The key to performance, always, is to not do things. And indeed, not doing much will be the path to our goal here, through an arcane concept called clipping.

I’d work all night if it meant nothing got done.

• Ron Swanson

Quick overview

Consider this situation, in which a window needs redrawing:

We can only see an L-shaped portion of it, clearly we don’t want to redraw more than that. It’s not easy copying an L-shape from a big array of pixels though, imagine the look of that for loop :)

This is why we’re going to cut up this L into rectangles, like this:

Much better, now this is something we can work with!

This whole “cutting stuff up into rectangles” is very visual, easy for us to do, but it’s not easy to see how to turn it into an algorithm. It’ll be some work, but it’ll pay off!

Implementation

As mentionned a few articles ago, this awesome series of articles will be the basis for SnowflakeOS’s implementation of clipping. Many thanks to the author!

Rectangle splitting

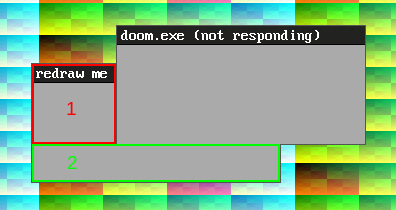
Our basic need is to be able to “split a rectangle by another”: given a rectangle to be split, R, and a rectangle that covers it S (for splitting rectangle), we want to get new rectangles, called clipping rectangles of R, satisfying the following conditions:

• their union must cover the area R \ S,
• they must be disjoint: no two of them should intersect.

In the above image for instance, “redraw me” was split by “doom.exe”, which produced two clipping rectangles, marked 1 and 2.

Clipping rectangles are never unique, but for our purpose they may as well be.

The core idea of the splitting algorithm is to examine each edge of S and check if it cuts through R. If it does, we have created a first clipping rectangle, and we can repeat the operation for the next edges, only now with a smaller rectangle to cut.

Here’s the algorithm:

list_t* rect_split_by(rect_t rect, rect_t split) {
    list_t* list = list_new();
    rect_t* tmp;

    // Split by the left edge
    if (split.left >= rect.left && split.left <= rect.right) {
        tmp = rect_new(rect.top, rect.left, rect.bottom, split.left - 1);
        list_add(list, tmp);
        rect.left = split.left;
    }

    // Split by the top edge
    if (split.top >= rect.top && split.top <= rect.bottom) {
        tmp = rect_new(rect.top, rect.left, split.top - 1, rect.right);
        list_add(list, tmp);
        rect.top = split.top;
    }

    // Split by the right edge
    if (split.right >= rect.left && split.right <= rect.right) {
        tmp = rect_new(rect.top, split.right + 1, rect.bottom, rect.right);
        list_add(list, tmp);
        rect.right = split.right;
    }

    // Split by the bottom edge
    if (split.bottom >= rect.top && split.bottom <= rect.bottom) {
        tmp = rect_new(split.bottom + 1, rect.left, rect.bottom, rect.right);
        list_add(list, tmp);
        rect.bottom = split.bottom;
    }

    return list;
}

Not an easy read, for sure. I won’t detail the list_t and rect_t types and associated functions, but you can trust that they do what they say. The list implementation can be found here, and operations on rect_t can be found here.

Some more convenient tools

The previous algorithm solves our previous situation perfectly, but suppose now that two windows cover the one we wish to redraw:

Say we split our window by “doom.exe 2”, and we get two clipping rectangles out of it. One of those is going to intersect with the “doom.exe 3” window, and this is no good, we’d be drawing a hidden part of the window.

What can we do? Well, let’s just split each one of our newly-acquired clipping rectangles by that second window! We’ll get a new list of clipping rectangles for each clipping rectangle intersecting with “doom.exe 3”… What we want is to keep only those new clips, and not the old ones. Well, there’s your algorithm.

To put it another way: given a list of clipping rectangles, and a splitting rectangle R, this algorithm punches an R-shaped hole in the area covered by the clips, while maintaining the two conditions listed previously.

The implementation is a bit easier to reason about this time:

void rect_subtract_clip_rect(list_t* rects, rect_t clip) {
    for (uint32_t i = 0; i < rects->count; i++) {
        rect_t* current = list_get_at(rects, i); // O(n²)

        if (!rect_intersect(*current, clip)) {
            continue;
        }

        rect_t* rect = list_remove_at(rects, i);
        list_t* splits = rect_split_by(*rect, clip);
        uint32_t n_splits = splits->count;

        while (splits->count) {
            list_add_front(rects, list_remove_at(splits, 0));
        }

        kfree(current);
        kfree(splits);

        // Skip the rects we inserted at the front and those already checked
        // Mind the end of loop increment
        i = n_splits + i - 1;
    }
}

The subtility is that we’re both removing and adding rectangles in our list of clips each iteration, so we need to keep a good track of where we are in our loop. The original author just set i = 0 at the end of the loop, which works great of course because the new clips we create never intersect with clip, but it wastes like, 30 clock cycles… :)

The cool thing with this new algorithm is that it superseeds the previous one entirely. Indeed, we don’t need a special case when we want to split a window: just put it in a list, and call the algorithm! Credit to the first one of course, it powers the whole thing.

It’s how you use it

Good, the hard work is done. We can draw stuff efficiently now, we have the technology!

Drawing a window

Consider our window’s rectangle. List all of the windows covering it, and punch a hole in the rectangle for each of them. Draw the areas of the window described by the clipping rectangles obtained. Simple as that!

Translated word for word^[2] in C:

void wm_draw_window(wm_window_t* win, rect_t rect) {
    rect_t win_rect = rect_from_window(win);
    list_t* clip_windows = wm_get_windows_above(win);
    list_t* clip_rects = list_new();

    list_add(clip_rects, rect);

    // Punch a hole for each covering window
    while (clip_windows->count) {
        wm_window_t* cw = list_remove_at(clip_windows, 0);
        rect_t clip = rect_from_window(cw);
        rect_subtract_clip_rect(clip_rects, clip);
    }

    // Draw whatever is left in our clipping rects
    for (uint32_t i = 0; i < clip_rects->count; i++) {
        rect_t* clip = list_get_at(clip_rects, i); // O(n²)

        // Fun edge case
        if (!rect_intersect(*clip, win_rect)) {
            continue;
        }

        wm_partial_draw_window(win, *clip);
    }

    rect_clear_clipped(clip_rects);
    kfree(clip_rects);
    kfree(clip_windows);
}

Notice the wm_partial_draw_window function call: it’s the only function that does any actual pixel work. It’s both mundane and insane (“the land of off-by-ones” you may say), and you can check it out here.

Drawing part of the screen

Imagine you’re closing a window. Then you have to redraw whatever was below that window, and that could be like, several windows. Do we redraw them entirely? Of course not, we can just redraw the parts of them that was covered by the closed window.

This is what led to the second parameter of wm_draw_window, i.e. a rect that says “draw within this area”. It’s used in the following short function that implements the redrawing of an area:

void wm_refresh_partial(rect_t clip) {
    for (uint32_t i = 0; i < windows->count; i++) {
        wm_window_t* win = list_get_at(windows, i); // O(n²)
        rect_t rect = rect_from_window(win);

        if (rect_intersect(clip, rect)) {
            wm_draw_window(win, clip);
        }
    }
}

What happens when a part of the screen you want to redraw isn’t covered by any window? As you may read above, nothing. Thankfully this doesn’t happen^[3], because there’s a huge window that draws the wallpaper… Ahem, I’ll get to it at some point ^^’

As a quick aside, you may have noticed the O(n²) sprinkled here and there in the code. Those are reminders for me to replace the list implementation I used: while really easy to use, iterating such a list automatically has quadratic complexity, which is obviously ridiculous. I doubt that it matters at all until you reach an absurd amount of windows, but it irks me a good bit. I’ll take Linux’s list.h to replace it, it looks just perfect.

Performance

Let’s see if we can get some numbers in here, check that all this work wasn’t in vain.

Our test will be spawning a hundred windows from a single process, plus the wallpaper. We will record the whole thing, and count the frames needed to go from a black screen to the 100^th window.

Before clipping, as of March 14th

It took 172 frames to get from the wallpaper to the last window, or 5.74 seconds.

After clipping

Now, it takes 11 frames, or 0.37 seconds. This is an improvement of about 1500%…

Mission accomplished!

We will for sure get smooth mouse movements and smooth window dragging in the next article now ^[4], until next time!